MATES: An Introduction to Tiling

MATES is a school publication organized by George School students who are enthusiastic about sharing their knowledge, inspirations, and passions in the five MATES subject areas—Mathematics, Arts, Technology, Engineering, and Sciences. MATES welcomes all students at all levels to share any thoughts about these five subject areas. Each article published explains the underlying truths behind intriguing theorems, patterns, phenomena, or artistic works and is carefully peer-reviewed and fact-checked.

The geometric idea of tiling, also known as tesselating, is for a shape or multiple shapes to be able to cover an entire 2D plane without overlapping or leaving any blank space. There are three main
ways to show this, all at least somewhat reliant on induction (as any problem dealing with the entire 2D plane would): repeatable constructions, construction of a shape that is already known to tile the plane, and the construction of a larger copy of the original shape, a special case of the first method. Here is an illustration of these with the three regular polygons that tile the plane.

The regular hexagon can be used for the first example. By the definition of regularity, these hexagons have equal side lengths on all sides, so they may be lined up vertically like so:

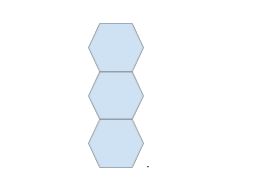
This may be repeated forever. Since each of the internal angles in each hexagon is 120 degrees, one additional hexagon may be wedged onto each of the intersection points of the existing hexagons:

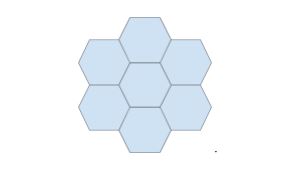
This expands the hexagon tiling horizontally, and, since each hexagon added vertically touches the intersection point of two other hexagons and shares a side with one, it must share a side with the other (because 240 degrees plus 120 degrees is 360 degrees). This allows for the tiling to be expanded vertically along with these new hexagons, as well:

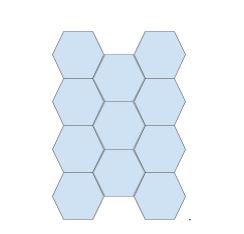
Since each of these new hexagon lines has the same attachment points as the previous one, this process may be repeated indefinitely to tile the plane.

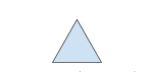
For the second example, an equilateral triangle will be used. Six equilateral triangles may be combined to form a regular hexagon as follows:

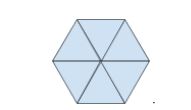
As such, this problem reduces to the already-solved problem of tiling the plane with hexagons.

For the final example, a square will be used. Since squares have equal side lengths, they may be arranged like so:

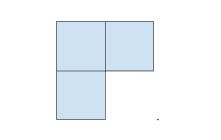
From here, an additional square can be attached. This square does not overlap due to the fact that 360 degrees equals four times 90 degrees:

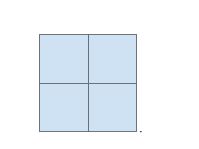
This is a larger version of the previous square, with side lengths double that of the original. As such, each of these larger squares can undergo the same process as the original:

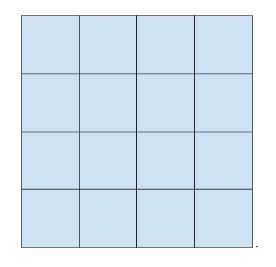
As this may be repeated to arbitrary size, this is a valid tiling. In terms of why only these three tilings of regular shapes are allowed, the angles must be a factor of 360 degrees. Otherwise, there would either be gaps or overlap. For instance, the regular pentagon cannot tile the plane, as its angles are not factors of 360 degrees:

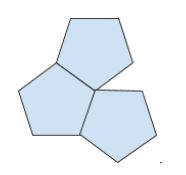
Because regular hexagons, squares, and equilateral triangles are the only regular polygons with angles that are factors of 360 degrees, they are the only regular polygons capable of tiling the plane.
However, non-regular polygons may also tile the plane. Take the case of an arbitrary triangle.

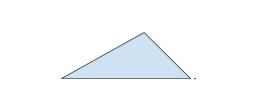
Though irregular, this shape may be rotated 180 degrees and attached to form a parallelogram:

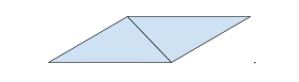
This parallelogram may then be extended horizontally:

Since both the top and bottom of this line of parallelograms is a straight line, these may be stacked indefinitely, tiling the plane:

Additionally, multiple shapes may be used, such as this tiling involving both octagons and squares:

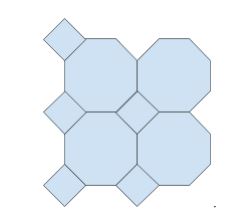
Some ideas beyond the scope of this introduction but interesting nonetheless are aperiodic tiling, such as Penrose Tilings(1), where there is no overarching pattern and higher-dimensional tilings, such as those discovered by Conway, Jiao, and Torquato involving octahedra and tetrahedra. (2)

—

1: Schultz, K. Penrose Tilings. The University of Georgia.
http://jwilson.coe.uga.edu/emat6680fa05/schultz/penrose/penrose_main.html. Accessed 18 May 2021

2: Conway, J. H., Jiao, Y., & Torquato, S. (2011, July 5). New family of tilings of three-dimensional Euclidean space by tetrahedra and octahedra. PNAS. National Academy of Sciences.
https://www.pnas.org/content/108/27/11009. Accessed 18 May 2021

Zach’s interests fall into the mathematics and science (physics) categories of the MATES subject areas (which include Mathematics, Arts, Technology, Engineering, and Science(s)). His submission to the first edition exemplifies his ability and enjoyment of imaging geometries. His article starts from the most simplistic geometries and gradually leads the audience into the beauty of tiling.

Read more.